Niels Bohr fue un físico nacido el 7 de octubre de 1885 en Dinamarca, que consiguió el premio Nobel de física en 1922. Entre sus logros se puede destacar el primer desarrollo del esquema del átomo con protones y neutrones, y electrones rodeándolos. Gracias a sus contribuciones, se convirtió en un pionero de la teoría cuántica.

Según Ernest Rutherford (barón Rutherford de Nelson o Lord Rutherford), que era presidente de la Sociedad Real Británica y Premio Nobel de Química en 1908, ocurrió una situación anecdótica cuando Niels Bohr era jovencito y estudiaba bajo su tutela.

Esta es una historia que viene a demostrar la gran inteligencia de este hombre, amén de las buenas costumbres que nos pueden inculcar en la enseñanza para aprender a pensar y desarrollar de varias formas un problema de resolución evidente.
El suceso verídico empieza así:
“Hace algún tiempo, me llamó un colega. Se encontraba en la tesitura de poner un cero a un estudiante por cierta respuesta que había dado en un problema de física, y el estudiante seguía afirmando que su respuesta era correcta. Los profesores y estudiantes convenieron pedir arbitraje de alguien que fuese imparcial y yo fui elegido.
Me dispuse a leer la pregunta del examen que decía: Demuestre cómo es posible hallar la altura de un edificio ayudándose de un barómetro. El estudiante respondió lo siguiente: llevamos el barómetro a la azotea de dicho edificio y le atamos una cuerda muy larga. Lo descolgamos hasta la base del edificio, marcamos y medimos. La longitud de la cuerda establecida, es igual a la longitud del edificio.
En realidad el alumno había propuesto un grave problema al resolver el ejercicio de esta forma, ya que había solucionado la pregunta de manera acertada y completa.
Por otro lado, si se le otorgaba la máxima puntuación, podría modificar el promedio de su año estudiantil, conseguir una nota mas alta y así legitimar su alto nivel en física; pero la solución hallada al problema no aseguraba que el estudiante poseyera ese nivel.
Entonces propuse que se le concediera otra oportunidad al alumno. Le proporcioné 6 minutos para que contestara a la misma pregunta, pero esta vez tenía la condición de que en la respuesta debía revelar sus conocimientos de física.

Cuando habían pasado 5 minutos, el alumno seguía sin haber escrito nada. Le pregunte si quería irse, pero me contesto que tenia varias respuestas al dilema. Seguía dudando en cuál podría ser la mejor de todas. Me disculpé por la interrupción y le rogué que siguiera.
En el último minuto que le quedó, escribió la siguiente solución: tomamos el barómetro, lo lanzamos al suelo desde la azotea del edificio y calculamos el tiempo de caída con un cronometro. Después aplicamos la formula altura = 0,5 por A por t^2. Y de esta manera hallaremos la altura del edificio.
En ese momento le consulté a mi colega si el alumno podía abandonar la sala. Le concedió la puntuación más alta de todas.
Cuando me marché del despacho, me volví a encontrar con el alumno y le solicité que me contara sus otras soluciones a la pregunta. Bueno, contestó, hay muchas formas. Por ejemplo, tomamos el barómetro en un día que haga sol y medimos la altura del barómetro y la longitud de su sombra. Si se mide a continuación la longitud de la sombra del edificio y se aplica una simple proporción, podremos hallar también la altura del edificio.
Perfecto, le contesté, ¿y de otra forma?. Si, me dijo, ésta es una técnica muy simple para medir un edificio, pero también nos puede servir. Para este sistema, debemos tomar el barómetro y nos situaremos en las escaleras del edificio en la planta baja. Según vayamos subiendo las escaleras, iremos marcando la altura del barómetro y contaremos el numero de marcas hasta llegar a la azotea. Si multiplicamos al final la altura del barómetro por el número de marcas que hemos realizado, también tendremos su altura.
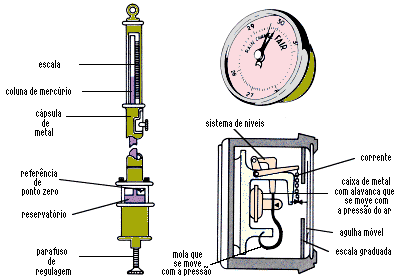
Este es un procedimiento muy directo. Pero si queremos un recurso más elaborado, podemos atar el barómetro a una cuerda y realizar movimientos como si fuese un péndulo. Si se calcula que cuando el barómetro se encuentra a la altura de la azotea la gravedad es cero, y tenemos en cuenta la magnitud de la aceleración de la gravedad al descender el barómetro en el itinerario circular al cruzar por la perpendicular del edificio, de la diferencia de estas estimaciones, y si aplicamos una simple fórmula trigonométrica, podemos hallar, sin duda alguna, la altura del edificio.
Siguiendo un patrón parecido de sistema, atamos el barómetro a una cuerda y lo descolgamos desde la azotea a la calle. Si lo empleamos como un péndulo, podemos calcular la altura midiendo su período de precesión.
Concluyendo, se pueden encontrar otras muchas maneras. Seguramente, la mejor sería cogiendo el barómetro y golpeando con él la puerta de la casa del portero. Cuando éste abra, le diremos: “Señor portero, aquí tengo un espléndido barómetro. Si usted me puede decir la altura de este edificio, se lo regalaré”.
En ese preciso instante, le pregunte si no sabía la respuesta más común al problema (la diferencia de presión que nos marque un barómetro en dos lugares distintos, nos facilitará la diferencia de altura entre ambos sitios). Obviamente dijo conocerla, pero también me contó que durante sus enseñanzas, sus profesores habían procurado enseñarle a pensar.”
Evidentemente, este joven era Niels Bohr.





Qué suerte tuvo al cruzarse con profesores que le enseñasen a pensar. Los míos sólo me enseñaron a coger al dictado todo lo que ellos dijeran lo más literalmente posible, aprendérmelo de memoria lo más rápidamente posible y vomitarlo en el examen lo más fielmente posible. pero claro, yo hice Derecho…
gracias por hacerme reir, fabuloso, no lo conocía, jaja fantastic.
Me ha recordado una anécdota en la facultad de ciencias de Granada, ocurrió cuando mi profesor me cogió de la mano por el pasillo y me arrastraba al despacho coméntandole a una colega que había 3 tipos de respuestas a los problemas, la que el explica en clase, la que los alumnos hacen en el examen (que está mal), y la que yo presentaba de vez en cuando.
No sé como lo ha hecho pero está bien, es el único que lo ha sacado y lo apruebo solo por eso.
Me llena de orgullo pese a que soy un desastre y nunca acabaré mi licenciatura.
Pensar diferente es lo máximo, ser capaz de ver lo que otros no pueden es una sensación comparable a un orgasmo, sin embargo trae muchos problemas, es como estar enamorado de la mujer que no te conviene, una lucha sinfin,… perdona que estropee tu artículo, yo no soy nadie y este Bohr es palabra de dios, gracias por enseñarmelo.
Estupendo, cuando uno es maestro lo mejor que puede pedir al alumno es que piense pero de no de forma convencional sino razonativa como lo hizo Niels Bhor, a eso se le conoce como metacognición, son personas brillantes en su raciocinio lógico.
Excelente post. Muy instructivo y muy ameno.
Saludos, y felicidades por el blog.
Pues se pasó de listo porque lo único que le dieron para resolver el problema fue un barómetro. Según el enunciado del problema, no disponía ni de un cronómetro con el que medir el tiempo de caída, ni de una cuerda, ni de un metro para medir el barómetro o para medir la sombra que proyectaba este… así que le deberían haber puesto un cero. los profesores siempre lo dicen, hay que leer bien las preguntas de los exámenes.
A por cierto el otro día le pregunté al portero del edificio cuál era la altura del edificio en el que vivo y lo único que me contestó es que tenía 12 plantas, que no se sabía la altura. Un saludo.