Iniciemos este recorrido escarpado meditando sobre la siguiente disyuntiva borgesiana: supongamos que para formar palabras se pueden usar todas las combinaciones de las veintisiete letras del abecedario (y que, en particular, no haya problema alguno con las palabras sin vocales). Más aún, imaginemos que tenemos una copia del diccionario de todas las palabras posibles en nuestras manos. Ciertamente, sería lógico dividir este inmenso diccionario en veintisiete tomos, cada uno de los cuales corresponda a la primera letra de las palabras que figuran en él.

Pues bien, como todas las palabras del tomo correspondiente a la letra «a» comienzan con la letra «a», resultaría totalmente natural borrar esta primera letra de cada palabra allí listada, pues se trata de información redundante. Al hacer esto, ¿con qué nos quedamos? Basta meditar un instante para adivinar: hemos recuperado una copia exacta del diccionario original. Haciendo lo mismo con los tomos de las letras «b», «c»,… obtenemos veintisiete tomos iguales. Así, el diccionario de todas las palabras es igual a veintisiete copias idénticas de sí mismo.
Todo lo anterior es absurdo, pues la cantidad de palabras en cuestión sería infinita y, por lo tanto, el diccionario de todas las palabras no puede tener materialidad alguna.
Muy bien, pero, ¿habrá alguna forma de conferir una geometría a esta paradoja? Tal fue la pregunta que se hicieron a inicios del siglo XX el alemán Felix Hausdorff y, posteriormente, los polacos Stephan Banach y Alfred Tarski.
Felix Hausdorff.

Basándose en una idea del primero, los dos últimos dejaron estupefacto al mundo académico cuando, en 1924, anunciaron el siguiente teorema: «Una pelota de cualquier radio puede ser descompuesta en una cantidad finita de partes que, al ser reensambladas, originan dos pelotas del mismo radio que la original». La matemática conseguía probar así que la Biblia tiene razón: ¡el milagro de la multiplicación de los panes y de los peces (o, en nuestra formulación, de las pelotas) es factible!

Esto es una total estupidez, pues no se puede crear masa a partir de la nada.
Sin embargo, en nuestra elucubración debemos desprendernos de toda consideración física. La masa, los átomos, las moléculas, el vacío, la nada, todas son nociones que deben estar ausentes de nuestro raciocinio ya que, en el universo matemático, el espacio está compuesto de puntos que son indistinguibles unos de otros. Es en parte por esta razón que los caminos de la lógica pueden llevar a la matemática hacia terrenos insospechados, los que a veces la alejan de la realidad física.
Bien, pero el concepto de volumen sí es matemático, y la afirmación de Banach y Tarski implica la creación de volumen, lo cual sigue siendo absurdo.
Buen argumento, pero justamente lo que se está revelando es que no se puede asignar un volumen a todos los subconjuntos del espacio. Las partes en que debe ser dividida una bola para equirrepartirla en dos bolas de igual radio a la original son complicadísimas «nubes» de puntos que no poseen volumen. Entiéndase bien: no se trata de que su volumen sea igual a cero, sino de que simplemente ¡no tienen volumen!
Muy bien, ahora puede parecer verosímil, pero ¿cuáles son, por ejemplo, las partes en las que se descompone una pelota de radio 1 que se reensamblan en dos pelotas del mismo radio?
Muy perspicaz pregunta. De hecho, resulta imposible dar una descripción explícita de los conjuntos involucrados. Hacerlo contravendría uno de los cimientos lógicos sobre los cuales reposa gran parte de la matemática y que preferimos no poner en cuestionamiento.
Esta piedra angular, a la que denominamos «axioma de elección», corresponde a una cierta potestad huidobriana de «pequeños dioses» que nos autoconferimos y que dice simplemente que, si tenemos familias de conjuntos, entonces podemos escoger un miembro de cada una de ellas.

A grandes rasgos, las partes involucradas en la descomposición de Banach-Tarski de una pelota corresponden a elecciones abstractas en familias de puntos infinitas, lo cual les da un aspecto «nebuloso» e impide que se las pueda describir verbalmente. Hacerlo provocaría, simplemente, un colapso del universo lógico…
Aunque el axioma de elección puede parecer evidente, lo cierto es que no lo es cuando hay infinitas familias de conjuntos involucradas, y ellas son además infinitas. De hecho, ha habido quienes —los así llamados «intuicionistas»— lo han puesto en cuestionamiento y han desarrollado una matemática «paralela» en la cual deja de tener validez, y en la que la descomposición de Banach-Tarski es imposible.
Bien —suena intimidantemente convincente—, pero, ¿puede hacerse lo mismo con un círculo del plano en lugar de una pelota?

Otra perspicaz pregunta; para ella, la respuesta es negativa. Un aspecto crucial de la construcción de Banach y Tarski consiste en explotar la riqueza de los movimientos rígidos del espacio tridimensional, que son muchísimo más complejos que los del plano. A modo de ejemplo, dos rotaciones del plano centradas en un mismo punto siempre están relacionadas, pues si aplicamos una y luego la otra obtenemos el mismo resultado que si invertimos el orden de aplicación: «el orden de los factores no altera el producto».
Sucede que en el espacio tridimesional esto deja de ser verdad. Si bien las rotaciones con un eje común están relacionadas como anteriormente, existen pares de rotaciones que no tienen relación alguna entre ellas. Es como si, al considerar el diccionario geométrico cuyas palabras corresponden a elecciones al azar entre una y otra rotación, todas esas fuesen distintas, y no se tuviese por ejemplo la relación ab = ba de las rotaciones del plano centradas en un mismo punto.
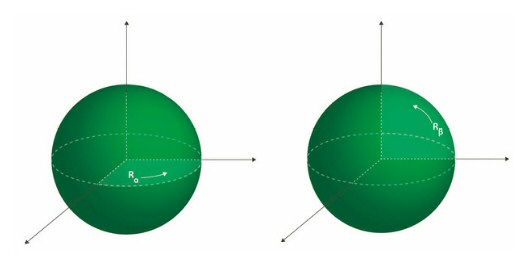
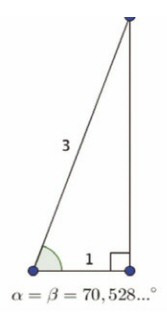
Así, para las rotaciones en tridimensionales, ¡el orden de los factores sí altera el producto! La rotación de ángulo α en un plano horizontal y de ángulo β en un plano vertical representadas más arriba no verifican ninguna relación algebraica si α y β son bien escogidos (y «poco convencionales»). Esto se cumple, por ejemplo, si α = β coinciden con el ángulo descrito en la figura de abajo, el cual —medido en grados— es irracional.
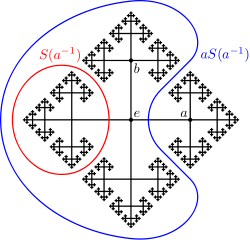
Gozamos así de la «libertad» necesaria para ejecutar nuestra «paradoja» inicial. En efecto, pese a que el diccionario de todas las palabras (en un alfabeto de apenas dos letras) no existe físicamente, si tomamos un punto en la pelota y consideramos todos los puntos a los que va a parar usando nuestras dos rotaciones «libres», estos puntos quedan codificados cada uno con una palabra de dicho diccionario.
Como esta acción puede ser ejecutada con cualquier punto, la pelota entera puede ser pensada como una amalgama de infinitos diccionarios de dos letras cada uno. Ejecutando entonces nuestra partición borgesiana de cada uno de estos diccionarios, se puede fácilmente completar la ejecución del milagro de multiplicar una pelota en dos pelotas iguales.
A la izquierda: Stephan Banach. A la derecha: Alfred Tarski.


Banach fue el patriarca de una brillante generación de matemáticos polacos que tuvo un final abrupto con el advenimiento de la Segunda Guerra Mundial. Y si bien él logró sobrevivir a la ocupación nazi, murió en 1945 producto de un cáncer desarrollado en esos años.
Tarski tuvo «mejor» suerte. Pese a que buena parte de su familia pereció en la guerra (su ascendencia era judía), logró emigrar a Estados Unidos en 1939. Dictó clases en Berkeley y Harvard, desde donde cimentó una escuela de lógica y filosofía de enorme trascendencia.
Entre sus discípulos se cuenta un chileno, Rolando Chuaqui, quien, aunque defendió una tesis en probabilidades dirigida por el matemático de ascendencia africana David Blackwell, fue profundamente influenciado por su obra. La conjetura de Chuaqui, resuelta por el polaco Piotr Zakrzewski en 1991, era una suerte de afirmación recíproca de la paradoja de Banach-Tarski: someramente, el que un objeto no admita una descomposición paradojal implica que a todos sus subconjuntos se les puede asociar un volumen apropiado.
En memoria de Chuaqui se celebran cada año las jornadas homónimas de filosofía. Además, con su nombre fue bautizado el edificio de la Facultad de Matemática de la Pontificia Universidad Católica de Chile, diseñado por Alejandro Aravena.
Fue de esta forma que las ideas de Tarski, al igual que las de un buen maestro y profeta, se fueron multiplicando por el mundo entero como panes y peces.