Partes del especial «El modelo estándar y el bosón de Higgs»
Parte 1: El Modelo Estándar
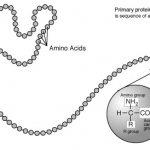
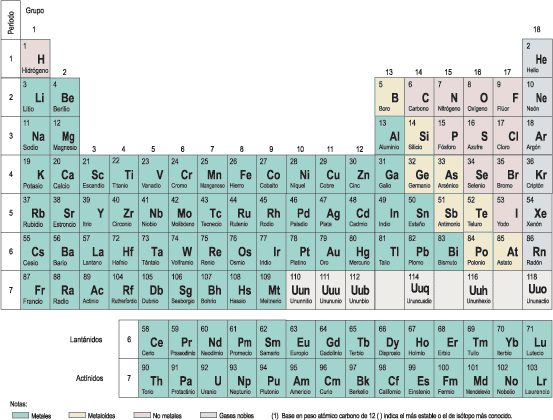
Parte 2: Constituyentes básicos de la materia
Parte 3: Interacciones básicas
Parte 4: Simetrías básicas
Parte 5: Masa contra simetría
Parte 6: El mecanismo de Higgs
Parte 7: Una imagen sencilla
Parte 8: Ruptura espontánea de la simetría
Parte 9: Ruptura electrodébil
Parte 10: Al comienzo del universo…
En el especial «La masa en la ciencia«, introdujimos la idea de simetría aplicada a las ecuaciones básicas de la naturaleza. Recordemos: una simetría de esas ecuaciones es una transformación matemática que las deja idénticas a sí mismas. También mencionamos algunas simetrías importantes, por ejemplo la invariancia bajo traslaciones espaciales y temporales. Y recordamos que Emmy Noether nos enseñó que las simetrías conducen a leyes de conservación, como el principio de conservación de la energía.
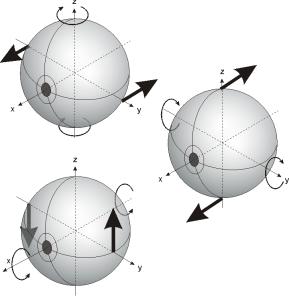
Todas las simetrías hasta ahora mencionadas poseen algo en común: tienen que ver con transformaciones del sistema de referencia espacio-temporal (trasladándolo, rotándolo o poniéndolo a una cierta velocidad). Pero podemos imaginar transformaciones en las que mantenemos el sistema de referencia espacio-temporal fijo y, sin embargo, modificamos imaginariamente el valor de los campos. Si encontramos una manera de hacerlo, de forma que las ecuaciones queden invariantes, habremos encontrado una nueva simetría. Pronto ilustraremos esta idea con un ejemplo.
A este tipo de simetrías se les llama simetrías internas, y también implican leyes de conservación. Por ejemplo, la conservación de la carga eléctrica (y el propio concepto de carga eléctrica) proviene de una simetría interna que presentan las ecuaciones del Modelo Estándar. Jamás se ha observado un proceso en el que se viole este principio de conservación, por ejemplo, dos electrones (ambos de carga negativa) aniquilándose y produciendo dos fotones. Hay una simetría detrás que lo impide. Las simetrías son ciertamente poderosas para explicar aspectos esenciales de la naturaleza.
Hay un tipo especial de simetrías internas que conlleva no solo un principio de conservación asociado, sino algo más… y de una importancia extraordinaria. Estas son las llamadas simetrías locales (a menudo llamadas simetrías gauge, usando la jerga inglesa). Una simetría local es sencillamente una simetría en la que el valor del campo se puede modificar de forma distinta en cada punto del espacio. Enseguida veremos un ejemplo de una simetría de este tipo.
Pero, antes, vamos a decir por qué son tan importantes. La razón es que puede demostrarse que una simetría local conlleva necesariamente una interacción asociada. Este hecho esencial fue descubierto por Yang y Mills en 1954, quienes describieron teóricamente cómo es la interacción en cuestión dependiendo de la simetría local de la que provenga.
En todos los casos la interacción está transmitida por partículas mediadoras de espín entero (casi siempre espín 1, con alguna excepción) y con masa cero… ¡exactamente como ocurre en la naturaleza!, aunque en 1954 estos hechos solo estaban bien establecidos para la interacción electromagnética, transmitida por fotones. Existía una gran confusión en aquella época sobre la naturaleza de las interacciones fuertes y débiles. Hoy sabemos que las cuatro interacciones fundamentales provienen de simetrías locales asociadas.
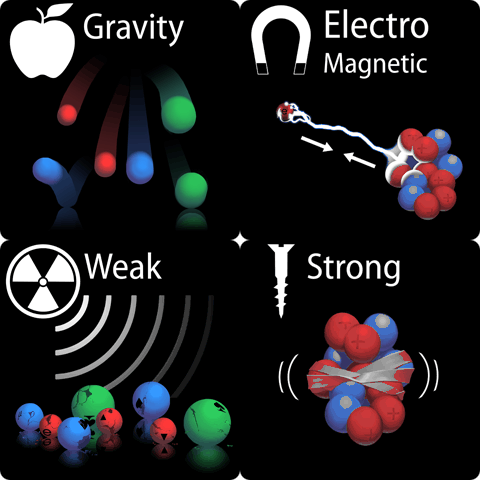
Este es uno de los aspectos más satisfactorios del Modelo Estándar. La perspectiva moderna no es que la naturaleza haya decidido por algún motivo presentar cuatro interacciones básicas que resultan «casualmente» estar mediadas por partículas mensajeras de espín entero y masa nula. La perspectiva moderna es que la naturaleza ha decidido por algún motivo poseer algunas simetrías básicas, y de ahí se deducen una serie de implicaciones.
Y una de las implicaciones más importantes es la existencia de interacciones, con la forma dictada por la propia simetría subyacente. Por supuesto, ahora podemos preguntarnos: ¿por qué la naturaleza ha elegido tener precisamente las simetrías que tiene? En efecto, esta es una pregunta fundamental de la física teórica actual, y de momento no tenemos respuesta convincente para ella.

El hecho de que las simetrías locales conduzcan a la existencia de interacciones es tan importante que merece la pena entenderlo con más profundidad. Para ello, vamos a imaginar un modelo simplificado de universo, en el que este solo tiene dos puntos: x1 y x2; tal como muestra la figura anterior.
Por supuesto, este modelo de universo es completamente irreal, pues el auténtico tiene infinitos puntos, pero nos sirve para ilustrar la idea. Supongamos ahora que en este universo minimalista existe un campo, que representamos con la letra griega φ (fi). Al tratarse de un campo, tomará un valor en x1 digamos φ (x1), y otro en x2, o sea φ (x2); tal como representa la figura anterior.
La evolución del campo φ con el tiempo estará determinada por alguna ecuación, que será la ecuación básica de este universo de juguete. No nos hace falta escribir la forma que podría tener esa ecuación, simplemente imaginemos que depende de la diferencia del valor del campo en los dos puntos, o sea, de la cantidad φ (x1) − φ (x2). De hecho, algo muy parecido ocurre en las ecuaciones auténticas del universo de verdad. Ahora podemos explorar si esta ecuación posee alguna simetría. Y efectivamente la tiene. Hagamos la transformación:
φ → φ + q
Es decir, en todos los sitios donde ponga φ (sea en el punto x1 en el x2) ponemos ahora φ + q (q es un número cualquiera). Esta transformación corresponde a una simetría, ya que la cantidad φ (x1) − φ (x2), que es la que aparece en la ecuación, no sufre modificación:
φ (x1) − φ (x2) → φ (x1) − φ (x2)
Por tanto la ecuación básica queda como estaba. Notemos que se trata de una simetría interna, ya que no modificamos ni el espacio (en este caso, las posiciones x1 y x2) ni el tiempo, solo el valor del campo. Pero esta no es una simetría local, ya que hemos supuesto que el campo φ sufre la misma transformación en los dos puntos de nuestro universo en miniatura.
Exploremos si esta simetría puede ser también local; es decir, supongamos ahora que el valor de q es diferente para cada uno de los dos puntos. La transformación local tiene por tanto el aspecto:
φ (x1) → φ (x1) + q1
φ (x2) → φ (x2) + q2
donde q1 y q2 son dos cantidades que pueden ser distintas. Es fácil darse cuenta de que ahora la ecuación no queda como estaba, ya que la cantidad φ (x1) − φ (x2) se modifica; concretamente:
φ (x1) − φ (x2) → φ (x1) − φ (x2) + q1 − q2
Por tanto, la ecuación no es invariante bajo la transformación local. No obstante, imaginemos que la naturaleza de este universo diminuto «ha decidido» que la transformación local es una auténtica simetría. Esto significa que hemos de cambiar la ecuación de alguna manera para que sea invariante. Y el truco para conseguirlo es añadir un campo nuevo a este universo, al que llamaremos campo A. Este campo se sitúa imaginariamente entre los puntos x1 y x2, como ilustra esta figura:

La idea es que el campo A también se transforma bajo la simetría local, de tal forma que contrarresta la falta de invariancia anterior. Concretamente suponemos que el campo se transforma así:
A → A − q1 + q2
Ahora cambiamos la ecuación que gobernaba la evolución del campo φ. Donde antes ponía φ (x1) − φ (x2) ahora escribimos φ (x1) − φ (x2) + A. Teniendo en cuenta cómo se transforma la combinación φ (x1) − φ (x2) y cómo se transforma A (véase las fórmulas de arriba) es fácil ver que la combinación φ (x1) − φ (x2) + A no se transforma en absoluto, permanece idéntica a sí misma.
Por tanto, la nueva ecuación sí es invariante bajo la transformación local. Esto lo hemos conseguido al precio de modificar nuestra ecuación de evolución original, introduciendo un nuevo campo, el campo A. En consecuencia, la evolución del campo φ depende ahora de lo que valga el campo A, y esto significa exactamente una interacción entre el campo φ y el campo A.
Es importante tener en mente que todas las propiedades de transformación que hemos escrito para los campos φ y A no significan modificaciones físicas de los mismos. Se trata solamente de transformaciones imaginarias, que formulamos matemáticamente sobre el papel. Cuando decimos que un cuadrado es una figura simétrica, eso significa que si lo rotamos imaginariamente 90° queda idéntico a sí mismo. Para imaginarlo no hace falta que lo rotemos físicamente.
Aquí sucede lo mismo. Lo que hacemos es una transformación imaginaria que deja la nueva ecuación idéntica a sí misma. Y hemos visto que, para conseguir esa invariancia, necesitamos un nuevo campo, el campo A, que interaccione con el campo original. Dado que trabajamos en el marco de una Teoría Cuántica de Campos, las excitaciones del campo A serán partículas elementales, distintas a las que provienen del campo φ. Ese nuevo tipo de partículas son simplemente las partículas mediadoras de la nueva interacción.
Lo extraordinario es que lo que acabamos de describir en nuestro universo de juguete parece ser lo que sucede en el universo real. Cada una de las cuatro interacciones básicas tiene exactamente las propiedades dictadas por la simetría que las origina. Esto supone uno de los avances más impresionantes de la física teórica en las últimas décadas y es parte esencial de la estructura del Modelo Estándar.
Por ejemplo, las propiedades de la interacción electromagnética, y la propia existencia de los fotones, y por tanto de la luz, provienen de la simetría que está detrás. Esa simetría es la misma que hace que existan cargas eléctricas conservadas. Matemáticamente es una simetría bastante simple: es equivalente a la que posee una circunferencia, que puede ser girada un ángulo arbitrario y permanece idéntica a sí misma.
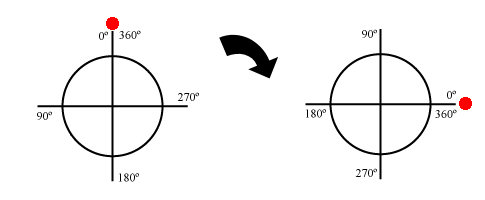
Más adelante volveremos sobre este concepto. Las propiedades de la interacción fuerte también provienen de su simetría, algo más grande y complicada que la electromagnética, y que en la jerga de los físicos se denomina color (nada que ver con el color ordinario de los objetos). Concretamente, hay ocho especies de gluones (recordemos: las partículas mediadoras de la interacción fuerte), tal como predice la simetría de color.
Asimismo, la simetría de color implica que la interacción fuerte entre dos quarks se hace más intensa a medida que se alejan uno del otro. Este hecho antiintuitivo es el que propicia el confinamiento de los quarks en partículas compuestas, como el protón y el neutrón. Más adelante hablaremos de la simetría correspondiente a la interacción débil (la gravitatoria se sale fuera del alcance de este artículo).
¿Por qué la naturaleza «ha decidido» poseer simetrías? La verdad es que no lo sabemos, pero pensemos en lo siguiente. Supongamos que en un universo alternativo imaginario las interacciones básicas tienen propiedades algo diferentes que las que tienen en el nuestro. Por ejemplo, las cargas eléctricas del mismo signo podrían atraerse y las de signo contrario, repelerse. ¡Esto es hacer auténtica «ciencia-ficción»!

Pues bien, las leyes físicas de ese universo no solo serían menos simétricas que las del nuestro, sino que sus ecuaciones presentarían ciertas inconsistencias matemáticas que más adelante comentaremos. Así que las simetrías no son solo bellas, sino tal vez indispensables para la coherencia interna de la teoría, es decir, de la naturaleza.