Leonardo Fibonacci nació en Pisa, Italia, en 1170, hijo de Bonacci (en italiano, figlio de Bonacci, o Fibonacci, nombre con el que se quedó).
Creció y fue educado en Bugia, norte de África (hoy llamada Bejaia, en Argelia), desde donde regresó a Pisa alrededor del año 1200. Fibonacci fue sin duda influido y posiblemente enseñado por matemáticos árabes durante este su periodo más formativo. Escribió muchos textos matemáticos e hizo algunos descubrimientos matemáticos significativos, lo que ayudó a que sus trabajos fueran muy populares en Italia y a que le prestara atención el Sacro Emperador Romano del momento Federico II. quien lo invito a su corte de Pisa. Fibonacci murió en 1250.
La secuencia de Fibonacci fue obtenida por primera vez en 1202, al tratar la cuestión del crecimiento de una población de conejos. Se hizo la pregunta de cuántas parejas de conejos habrá después de cierto número de temporadas de crianza, esto es, cómo se multiplican los conejos. Para simplificar supuso lo siguiente:
1) Se empieza con una pareja inmadura.
2) Los conejos maduran una temporada después de haber nacido.
3) Las parejas de conejos maduras producen una nueva pareja cada temporada de crianza.
4) Los conejos nunca mueren.
De acuerdo con estas reglas, el número de conejos en una generación es igual a la suma de las parejas de conejos que hay en las dos generaciones anteriores. Si se empieza con una pareja, después de una temporada se produce una nueva pareja. Por tanto, al final de la temporada hay 1 + 1= 2 parejas de conejos. Si se sigue de esta manera se encuentran los siguientes números de parejas en las sucesivas temporadas, que es precisamente la secuencia de Fibonacci.
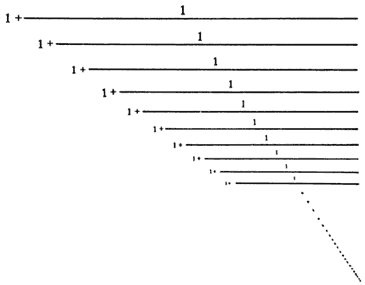
Simplificado, se empieza con 0 y 1, el siguiente número de la secuencia es la suma de los dos anteriores, y así sucesivamente.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, 1346269, 2178309, 3524578, 5702887, 9227465, 14930352, 24157817, 39088169…
La función se expresaría así:
F(n) = F(n-1) + F(n-2), F(0) = 0, F(1) = 1, F(2) = 1, …
Algunas particularidades en esta secuencia son:
– Un término de cada tres es un número par: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144…
– Uno de cada cinco es múltiplo de 5: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610…
– Cualquier número natural se puede expresar mediante la suma de un número limitado de términos de la sucesión de Fibonacci, y cada uno de ellos es distinto a los demás. Ejemplos: 18= 13+3+2 50= 13+34+3
– Si cogemos los números de la secuencia de dos en dos, y los dividimos entre sí, obtenemos con la progresión un acercamiento al cociente 0.618, el cual recibe el nombre de media dorada.
1/1=1 1/2=0.5 2/3=0.666 3/5=0.6 5/8=0.625 8/13=0.615 13/21=0.619 21/34=0.617
– En la naturaleza hay varios ejemplos de esta sucesión:
La cantidad de pétalos de una flor
La flor del girasol, por ejemplo, tiene veintiuna espirales que van en una dirección y treinta y cuatro que van en la otra; ambos son números consecutivos de Fibonacci.
La parte externa de una piña piñonera tiene espirales que van en sentido de las manecillas del reloj y otras que lo hacen en sentido contrario, y la proporción entre el número de unas y otras espirales tiene valores secuenciales de Fibonacci.
En las elegantes curvas de una concha de nautilus, cada nueva circunvolución completa cumplirá una proporción de 1: 1,618, si se compara con la distancia desde el centro de la espiral precedente.
La manera de reproducirse las liebres (la cantidad descendientes que tienen y cómo se “multiplican”).
Publicaciones relacionadas:
¿Cuál es el insecto con el ciclo vital de mayor duración? 
¿Qué es el diagrama de Venn? 
¿Por qué se emplea normalmente la X para expresar una incógnita? 
¿Por qué la Gran Muralla China tiene forma de zig zag? 
¿Tienen que ser gordos los cantantes de ópera? 
¿De dónde procede la costumbre de enterrar a los muertos?
Deberían ampliar un poco más el articulo y destacar cosas como la participación importante de esta secuencia a muchos más caso.
Por ejemplo el hombre de Vitruvio, la formación de los espirales, que se encuentran en toda la naturaleza, inclusive en los seres humanos etcetera.
Ampliar un poco más las caracteristicas curiosas de la sucesión.
Por ejemplo.
Si F(p) = a, tal que a es un número primo, entonces p también es un número primo, con una única excepción. F(4)=3; 3 es un número primo, pero 4 no lo es.
La suma infinita de los términos de la secuencia F(n)/10n es exactamente 10/89.
La suma de diez números Fibonacci consecutivos es siempre 11 veces superior al séptimo número de la serie.
El último dígito de cada número se repite periódicamente cada 60 números. Los dos últimos, cada 300; a partir de ahí, se repiten cada 1.5×10^n números.
La suma de los n primeros números es igual al número que ocupa la posición n 2 menos uno.
Y si se pudierá una breve menció de que TOOL la usa en su album Lateralus.
En el álbum Lateralus de la banda estadounidense Tool, los patrones de la batería (Danny Carey) de la canción Lateralis siguen la Sucesión de Fibonacci del número 13 (número de pistas del disco): 1,1,2,3,5,8,13,1,1,2,3,5,8,13,1,1,…
(bueno eso último es muy parcial hehe)
Tenía conocimiento de esa relación matemática, pero no sabía quién la había inventado.
Sin duda fue un genio.
Me parece muy interesante que se mencionen estas cosas pero si hablamos de la sicesión de Fibonacci me parecería tanmbien interesante hablar del número de oro, o Phi ( tambien de otras particularidades de la sucesión de Fibonacci que no vienen mencionadas)
Sin duda Phi es el número mas interesante del mundo,los digitos son infinitos e irrepetibles, porlo que me limitare a poner unos pocos que me se: 1,618033988749894848204586834365638117720309179805762862135448622705260462818902449707207204189391137484754088753868917521266338622235369317931800607667263544333898659593958290563832266131992829026788067520876689250171169620703222104321…etcétera
a primera vista no aprecias las propiedades de este número. primero decir que este número no es usado como tal, se usa en lo referente a proporción, y esta proporción es la que se encuentra en la serie de Fibonacci( aproximadamente, cuanto mas grandes sean lo números mas se acercara la proporción a Phi, pero como es un número infinito, nunca dara Phi exactamente)
Pero lo curioso no es esto simplemente, pongamos el caso del segmento de euclides, intentare dibujarlo
¡——–¡—–¡
A B C
parece un segmento normal, pero tiene una propiedad, ( me refiero al segmento de euclides, este es uno que hice yo a mano alzada).
imaginaros que la proporción del segmento total ( AC) entre la del segmento grande(AB) es la misma que la de el grande entre el pequeño(AB/BC) tal que AC/AB = AB/BC. Independientemente de la medida del segmento( ya que ablamos de proporciones) si esto se cumple el resultado siempre va a ser Phi, se dice que el segmento esta dividido en extrema y media razón o en proporción áurea.
Phi tiene mas curiosidades, imaginaros un número tal que el cuadrado del mismo sea igual al número mas uno, es decir:
x2 = x + 1 si esto fuera cierto, obtenemos que x2 – x – 1 = 0
y de esta ecuación obtenemos a Phi y como resultado negativo al inverso de Phi en negativo ( tambien se cumple que el inverso de Phi es lo mismo que Phi menos uno, es decir 0,6180339887…, a este número hay quien le llaman el hermano menor de Phi, y se escribe en minúsculas,»phi»)
al despejar la ecuación ( recomiendo que cojais un papel y un boli, es realmente curioso) obtenemos (1 + raiz de cinco)/2 como resultado positivo. 5 es un número curioso, guarda relación directa con Phi en esta ecuación, y es el primer número de la escala de Fibonacci que no es consecutivo al anterior. En esto no se tanto, pero estaría por decir que gracias a esto en un pentágono regular( polígono de CINCO lados) obtenemos que la relación entre la diagonal del pentágono y el lado del mismo es Phi.
si controlais un poco de trigonometría, podreis deducir porqué el coseno de 36 es la mitad de Phi y porque el seno de 72 entre el seno de 36 es Phi.
pero esta proporción no es un pretexto para sorprender, se encuentra en la naturaleza de manera natural, gracias a esta proporción el desarrollo de las especies frecuenta, en el artículo aparece que las espirales de los girasoles que van hacia un sentido y las que van hacia otro son números de Fibonacci ( por lo cual la suma de todas las espirales dará el siguiente número de esta sucesión). Pero parecería mas interesante saber el porqué de esta no coincidencia, y es porque de esta manera, se aprovecha al máximo el espacio circular del girasol ( si no cuando tengais uno en mano comprobar que no hay huecos, cosa que si que pasaría si la distribución fuera horizontal).
– en las hojas de ciertas plantas, apreciamos tambien esto, si os fijais en una hoja de la planta, y contais el número de hojas que hay entre una hoja y otra que este justo perpendicularmente encima de la misma, vereis que tanto este número de hojas como el numero de vueltas que das al tallo esta en la sucesión de Fibonacci.
– en las semillas de las plantas, nunca os habeis preguntado porqué las raíces de las plantas no se amontonan unas sobre otras?
la respuesta está en Phi:
la semilla es circular, si dividimos sus grados( 360º)entre Phi, aproximadamente da 222,5º, si ahora restamos 222,5º a los 360º de un círculo completo obtenemos 137,5º, que es el ángulo de separación entre las raices que nacen consecutivamente. Es gracias a esto, de una manera natural, que no se amontonan unas sobre otras y aprovechan mejor el terreno.
– la concha del nautilius: seguro que alguna vez visteis que la concha de un caracol tiene una espiral, pero esa espiral es una espiral áurea, que se obtiene de la siguiente forma:
a través de un rectángulo áureo( el lado mayor entre elmenor es Phi) o un triángulo áureo( triángulo isósceles cuya proporción entre un lado mallor y el menor, o el mallor entre uno menor es Phi) lo explicaré con un rectángulo áureo:
partimos de un cuadrado, del cual hacemos la mediatriz de un lado, y unimos este punto obtenido con uno de los vértices opuestos( obtenemos la semidiagonal el cuadrado). llevas esta medida, con centro en el punto de la mediatriz, a una prolongación del lado con el que trabajabas, obteniendo otro punto de corte
¡——-¡
¡ ¡
¡ ¡
¡——-¡—-¡
A B C
y obtenemos el segmento de euclides. Si levantamos una perpendicular desde el punto C y prolongamos el lado paralelo al que trabajabamos, obtenemos un rectángulo áureo, al cual, si le quitamos el cuadrado, tendríamos otro rectángulo de oro.
si seguimos con este proceso en los rectángulos áureos que se van formando( eliminando un cuadrado de lado igual al lado menor del rectángulo áureo) obtenemos infinitamente una serie de rectángulos áureos, y aciendo la espiral logarítmica, una espiral áurea
asi como aparece en la concha del nautilius, esta espiral forma diversas galaxias.
de alguna forma el numero Phi esta en la naturaleza porque la naturaleza asi lo pide
– en el vuelo de un halcón, supongamos que un halcón está justo encima de su presa, pongamos un ratón. Si efectivamente esta perpendicularmente encima, el halcón bajará haciendo una espiral áurea, y de ese modo, baja lo mas rápido posible manteniendo su vista siempre sobre la presa.
hay artistas que se aprovechan de esta proporción y la reflejan en sus obras de arte, Da vinci por ejemplo:
– en el cuadro de la mona lisa, la cara de la misma esta inscrita en un rectángulo de oro, al igual que en la última cena.
– en el hombre del vitrubio, da vinci forma al ser humano a partir de rectángulos áureos. Ya veo que Pablo lo menciona, solamente añadir que nunca es exactamente áureo el cuerpo humano( si efectivamente lo fuera, hablaríamos de un cuerpo perfecto)
La proporción áurea es importante en la construción de fractales, partamos de uno sencillo, supongamos que queremos crear un fractal a partir de triángulos equiláteros, construllendo otros triangulos equiláteros mas pequeños en los vértices del inicial. si la proporción que hay entre los triángulos mas pequeños a formar es 1/0,5 por ejemplo, las ramas de fractales no se llegaran a tocar entre si, esto solo sucedería si se van construllendo en proporción áurea ( 1/0,6180339887498948…)
Si alguien tiene una duda sobre lo que expliqué o le interesan los acertijos matemáticos y lógicos, aquí os dejo mi correo:
[email protected]
Un saludo
olaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa k tall?? estoy buskandoo la relacion que guarda la susecion fibonacci con el numero aureo..algien seriaa tan amablee de decirloo quee es muyy importanteeeee!! alijerarsee xfibo!
me parce que la unica relacion son los numeros naturales